Runge-Kutta methods of differential equation solvers


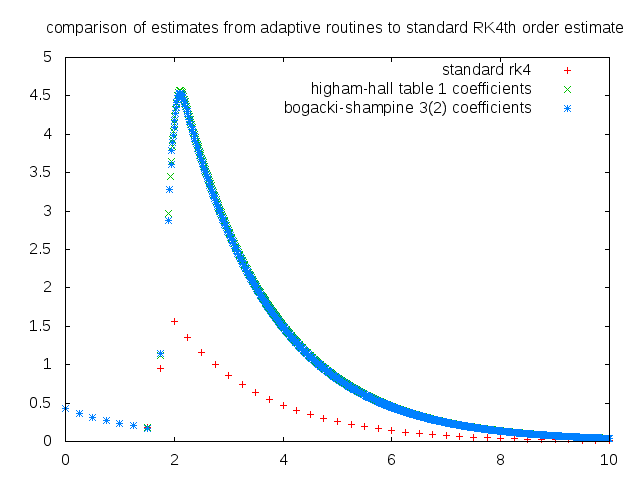
I knew that the difference would be large but not this large. Above is a plot of the estimates from a standard 4th order runge-kutta method compared with two other adaptive runge kutta routines. Adaptive runge-kutta routines vary the step size depending on the difference between mth order and nth order runge-kutta estimates, where m and n are usually 4 and 5. The Cash-Karp implementation of the runge-kutta fehlberg method, which is adaptive in nature, is one of the popular stepper routines in use. Each of these routines compares the error in the estimates from the nth and mth order routines with a preset tolerance and increase or decrease the step size appropriately. The above is a plot of the numerical solution of a first order ODE, the analytical solution to which is a narrow gaussian. And you can clearly see how wrong we are. The gaussian has a center at 2 and a width of 0.075 so one will have to start with a very small value to h to begin with, if one is interested in coming up with a simulation closer to reality. There were a couple of other comments made on my code so I guess we have a full plate.

Popular posts from this blog

Animation using GNUPlot

Image
Animation using GNUPlot I've been trying to create an animation depicting a quasar spectrum moving across the 5 SDSS pass bands with respect to redshift. It is important to visualise what emission lines are moving in and out of bands to be able to understand the color-redshift plots and the changes in it. I've tried doing this using the animate function in matplotlib, python but i wasn't able to make it work - meaning i worked on it for a couple of days and then i gave up, not having found solutions for my problems on the internet. And then i came across this site, where the gunn-peterson trough and the lyman alpha forest have been depicted - in a beautiful manner. And this got me interested in using js and d3 to do the animations and make it dynamic - using sliders etc. In the meanwhile, i thought i'd look up and see if there was a way to create animations in gnuplot and whoopdedoo, what do i find but nirvana! In the image, you see 5 static curv
Read more

Arxiv author affiliations using Python

So, I wanted to get author affiliation information from papers on arXiv. arXiv provides with an API to bulk query their database and get information. Following that, I look for the attribute 'arxiv:affiliation' in the html data. Here's the code - import urllib from BeautifulSoup import BeautifulStoneSoup   url = 'http://export.arxiv.org/api/query?search_query=all:astro&start=0&max_results=1000'   data = urllib.urlopen(url).read() soup = BeautifulStoneSoup(data) #print(soup.prettify()) #list = soup.findAll('arxiv:affiliation') #for i in range(len(list)): #        print list[i].contents   test = [tag.string for tag in soup.findAll('arxiv:aiffiliation')] Now, the problem I'm having is that I'm getting affiliation of all authors which I want to split into sets of affiliations of authors of a paper, which I'm stuck on at the moment. Once I get that part, I can move on to the next part of this pet project, displaying these
Read more

Thoughts on the National Deep Tech Startup Policy

The Principal Scientific Advisor to the Government of India published a draft policy to support and nurtue the unique requirements of Deep Tech startups in India. I just finished reading it and put together a few comments in a FOSS United forum thread . I will probably read it again a week or so later and try to update my comments on the thread with any new insights/thoughts I have.
Read more